|
Cryptography Challenge #64!
Link |
by
on 2011-01-24 17:45:50 |
|
This thread is for discussion of the Gendou.com Cryptography Challenge #64. Click the above link to view the challenge, get hints, and see the scoreboard. Please do NOT post spoilers! You may post your ideas and strategies, but no actual answers, ciphers, or code. 
|
|
Re: Cryptography Challenge #64!
|
|
Trying this challenge now, but I think I stuck already at some point... xD. Maybe you can show me what "AB" is in this cryptography? |
|
Re: Cryptography Challenge #64!
Link |
by
on 2011-01-25 10:42:49 |
AB: 
|
|
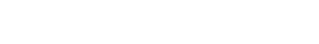
Re: Cryptography Challenge #64!
Link |
by
on 2011-01-26 13:00:27 (edited 2011-01-26 13:08:54)
|
|
Fermat... As in the guy who came up with the Last Theorem? I think I've read a book about him (title was "The Last Theorem") by Arthur C. Clarke. Didn't he write something like "I have a proof that's too large to fit the margin" or something...  |
|
Re: Cryptography Challenge #64!
Link |
by
on 2011-01-26 14:05:53 (edited 2011-01-26 14:06:16)
|
|
Yes, indeed! Once you finish the challenge, you'll see how it got it's name ;) Of course, solving it has nothing to do with Fermat's Last Theorem. Finding the solution to this challenge requires logical intuition, the ability to visualize shapes, and, of course, dedication!
|
|
Re: Cryptography Challenge #64!
Link |
by
on 2011-01-27 10:16:59 |
|
Man this one is something. I tried "distilling" the puzzle down to basic shapes, like the ones in your hints. But... I got into the same problem as in #62: trying to figure out which letters the shapes represent. In general, is there a specific "way" I'm supposed to think to dig out the alphabet? Delete this post if it's too helpful. |
|
Re: Cryptography Challenge #64!
Link |
by
on 2011-01-27 12:28:08 (edited 2011-01-27 12:28:29)
| ||||
A box is numbered in quadrants like this:
This is important for finding the cipher for the alphabet, as well as finding the "path" that the message takes. Alphabet Given 4 quadrants, there are 6 unique ways to select a subset of cardinality 2: P1 = { Q1, Q2 } (0011) P1 = { Q1, Q3 } (0101) P1 = { Q2, Q3 } (0110) P1 = { Q1, Q4 } (1001) P1 = { Q2, Q4 } (1010) P1 = { Q3, Q4 } (1100) So that yields 6 possibilities per square (split up into quadrants). Two squares yield 6 * 6 = 62 = 36 possibilities, enough for A-Z and 0-9! As you can see in the hints: A = P1 + P1 B = P1 + P2 C = P1 + P3 D = P1 + P4 ... Z = P5 + P2 Path Finding Starting with one square, you can't encode anything, because you need at lease 2 squares to encode the first letter. For this reason, there is a special "start encoding" state: P0 = { Q1, Q2, Q3, Q4 } (1111) From there, you can apply 2 characters of your message in the 4 resulting squares. Of course, if your message is only 1 character long, such as in hints 1 and 2, Q3 and Q4 are left blank. You know you've reached the end of a message when you see the "null terminator" state: Pend = Ø (0000) When the first 4 squares are used up, you will be left with 4 * 2 = 8 new squares to continue your message! This is a result of the fact that quadrants which are in the "on" state have been further sectioned into quadrants. Any time this happens, 2 of those quadrants may be filled, because we chose in the beginning to make subsets of 2 quadrants for P1 through P4! Neat, huh?
|
|
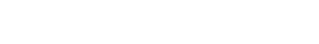
Re: Cryptography Challenge #64!
Link |
by
on 2011-01-27 15:06:54 (edited 2011-02-04 15:37:12)
|
|
Wow! I just glanced at that previous post, and it looks like there's a lot of useful information in there! Time to analyze it! Edit (2/4/11): I think there should be more than 7 people on this scoreboard at this point. I'll help a little bit (if this is too much, please delete this post): think about how an actual FRACTAL is made. I did it that way and I figured out the read order before Gendou-san put up his post. ;) Good luck everyone! |
|
Re: Cryptography Challenge #64!
|
|
Wow. I am glad I took a look here. I had the right idea but had all my 1's and 0's switched as well as my quadrants. Ugh, time to start over. Nice puzzle. I find it easier to encrypt things with this method rather than decrypt them, mainly to save my eyesight. |
|
Re: Cryptography Challenge #64!
|
| yah, i'd say that useful post is a little too useful... only spent 30 minutes once i saw the post |
|
Re: Cryptography Challenge #64!
Link |
by
on 2011-02-05 19:31:51 |
|
Haven't been here for a while now yep it's really easy with the "walkthrough" besides wrapping my head around the order of the recursive squares |
|
Re: Cryptography Challenge #64!
|
| Hi, I've made a puzzle similar to this one after knowing the basics of the pattern. I don't know how I can check if it's made correctly, so if possible, can you show me how "COLIN" would look like? |